在影片中3分03秒處計算重疊部分的長度時，Standupmaths said: “Now there is an argument …”，他認為重疊的長度 S 應該等於0.84公分
其實他算錯了，這一招屬於概略的估算，只適合使用在單選題中來快速找出正確的答案。因為右邊磚塊整塊向右平移到兩磚的角落恰好接觸時，左邊的磚塊其實又往下傾斜了一個小角度，使得這時的 θ’ 變大了
計算題應該是要這麼算才正確：下圖中的紅線長度是 √[(21-d)2 + (6sinθ)2 ]，其中 sinθ = √(1-cosθ2 ) = 0.96，即可算出紅線長度是 20.14公分，所以重疊部分為 0.86公分
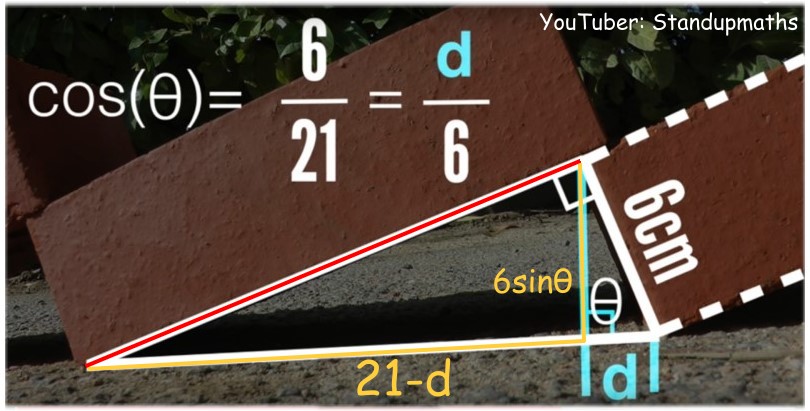這種可來回一趟的骨牌效應，返程會比去程快速。因為返程時所翻轉的角度小於去程，而且由於返程時重力所產生的力矩較大，因此(平均)角加速度就比去程來得大，造成每躺下一塊所需的時間就變短了
延伸閱讀
理論值是只要 4塊即可，不過很難達成，因為知易行難^^ →《疊硬幣遊戲》