先來看一段相關的影片
Derek Muller 對他所拍攝的影片做出如下的解釋
我的觀點則是:
這個重心遊戲可以使用熟雞蛋或是貼上黏土的硬幣來玩,魔術陀螺則可購自台北市一東玩具行(每顆15元)、鹿港的新大成藝品店(每顆10元)、高雄品美玩具行
科學原理:
魔術陀螺具有底部為圓形且重心低於其圓心的特性,旋轉這種陀螺時會由正立狀態變為倒立狀態,這是因為倒立旋轉才是它的穩定態。我曾測試了數十個陀螺之後,發現只有少數木柄安裝非常正的陀螺需要較長的時間才能發生進動,其餘大部分陀螺的木柄都會稍微傾斜或是偏離其軸線。這種重心偏離軸線的陀螺一旦開始旋轉之後,由於重心距離其轉軸的力臂不為零,因此陀螺所受的合力矩不為零,很快就能發生進動現象。
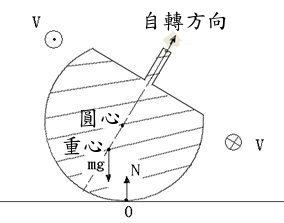
上圖為轉軸與鉛直方向偏離時的受力分析圖,此時陀螺受三個力的作用:重力 mg、正向力 N 與摩擦力 fr。重力mg過重心沿鉛直方向向下,正向力N垂直於地面沿鉛直方向過圓心,二者合力為零但合力矩不為零,此力矩就能形成陀螺的進動。同時,在支點處陀螺轉動的速度方向是進紙面方向,所以滑動摩擦力 fr 的方向就會與其相反而呈現出紙面方向,該力對自轉軸的力矩會減少陀螺轉動的角動量,使其自轉角速率變慢。另外,根據牛頓定律,滑動摩擦力f的方向與陀螺質心加速度的方向相同,因此摩擦力就會使陀螺整體以出紙面的方向加速移動。一般的陀螺發生進動時,其進動角速度的方向與原先直立狀態時的自轉角速度方向相同。魔術陀螺也是如此,從上面俯視時,木柄頂端是以逆時針進動旋轉。所以此時木柄頂端是呈現進紙面的運動方向,加上重心是出紙面的方向移動,這將使陀螺下一個接地點越發偏離底部向頂部的方向移動。而這時若觀察其底部接觸點,可發現支點移動的軌跡是繞著軸線中心點而形成螺線旋出。
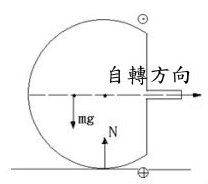
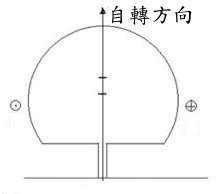
上圖中當陀螺轉軸偏離90度後,其狀態如右圖所示,此時重力mg與支持力N的合力矩達到最大。同時也在此時其進動角速率出現極大值,亦即從上俯視時,木柄以逆時針旋轉的頻率是最大的時刻。根據觀察,此時陀螺的自轉速率卻是接近為零,從角動量的觀點,這時候是不應該有自旋的。因為魔術陀螺一旦翻身後,其角動量方向仍然與初始時同樣向上,這表示對於陀螺本身而言,其自旋在翻身後卻是反向旋轉的。因此,當其轉軸由鉛直狀態逐漸偏離至水平的過程,其自轉速率變慢而進動速率變快。若是繼續翻身成倒立狀態而自身反向旋轉,那麼自旋速率為零確實應該發生在轉軸偏離90度的時刻,這就如同上拋的小球一定要先經歷速率為零的時刻才會反向運動一樣。陀螺水平橫躺時有最大的旋轉的頻率這也是合理的,因為初始狀態時的角動量是藉由滑動摩擦的協助,才能將自旋角動量轉換成進動角動量,也同時能將自旋動能轉換成進動的動能。這時候雖然陀螺幾乎不自旋,但重心卻是偏離正向力N的作用力線最遠,因此離心效應最明顯。再加上先前重心有向上方移動的動能,此後重心將繼續上升而造成接地點越來越往柄端靠近。
上述過程持續進行而致使與桌面的接觸點移動到木柄的頂端時,如果此時新接觸點的摩擦力足以頂住支點時,重心就能藉此瞬間攀高,使支點一下子由球面跳到木柄的頂端。而此後陀螺的運動就和一般的尖腳陀螺就沒甚麼不同,也就是形成一個比較穩定的狀態了。由於這種陀螺以木柄在上而重心低於圓心的旋轉是不穩定的,因此它能自動地反轉為倒立狀態,故又稱為可倒立陀螺或翻身陀螺。這顆玩具雖小卻有著大學問,就連諾貝爾物理大師 Pauli & Bohr 都對它能翻身充滿著好奇呢!